About Me
I am a doctoral student at the Royal Institute of Technology (KTH or Kungsliga Tekniska Högskolan in Swedish), working on machine learning for reactor physics applications (expected 2025). Previously, I worked in the Singapore Nuclear Research and Safety Initiative (SNRSI) for 3 years, as a researcher in the field of computational neutron transport method development.
I obtained my Masters of Engineering degree from UC Berkeley in the department of Nuclear Engineering and my Bachelors of Engineering from the National University of Singapore in Chemical Engineering (First Class Honours). I have a broad research interest in applied machine learning methods and the development of specialized AI and machine learning applications.
Connect with me if you are interested in collaborating! My contact information can be found under the “Contact” tab, together with my full CV.
On this site you will find short summaries of the publications which I worked on. The key projects are featured below. More detailed summaries of my publications can be found under the “Posts” tab.
Featured Projects
MAREN
MAchine learning based REpresentation for Nuclear cross-section libraries
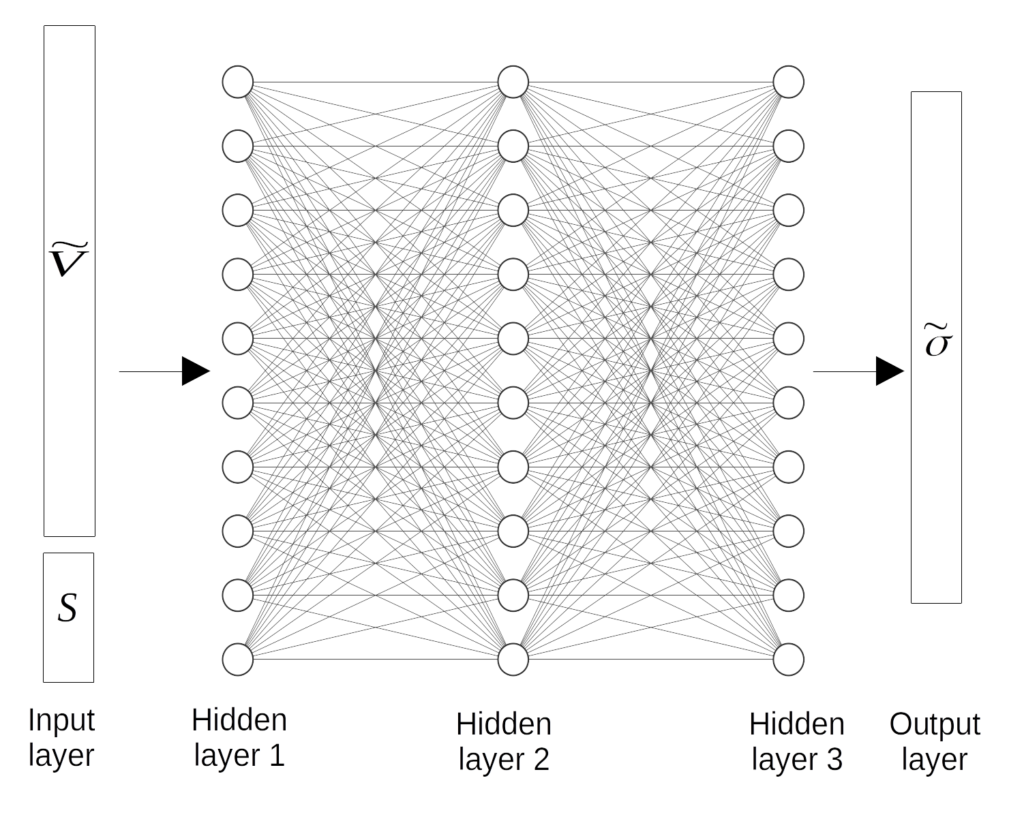

High dimensional cross-section libraries are used in deterministic neutron transport codes for various applications. These libraries contain 10s-100s of energy groups of numerous nuclides’ cross-section data. These values are dependent on reactor operating conditions and on fuel isotopic compositions.
Implementing a regression model to map the input parameters (~10s of parameters) to the output space (~1000s of parameters) is a challenging computational problem. We showed that the use of Principal Component Analysis (PCA) to perform dimensionality reduction combined with fully connected Deep Neural Networks (DNNs) were able to efficiently perform this regression task. More details on the specific publications can be found in the following links:
Computational neutron transport method development
Theoretical and practical extensions of the lp-CMFD method
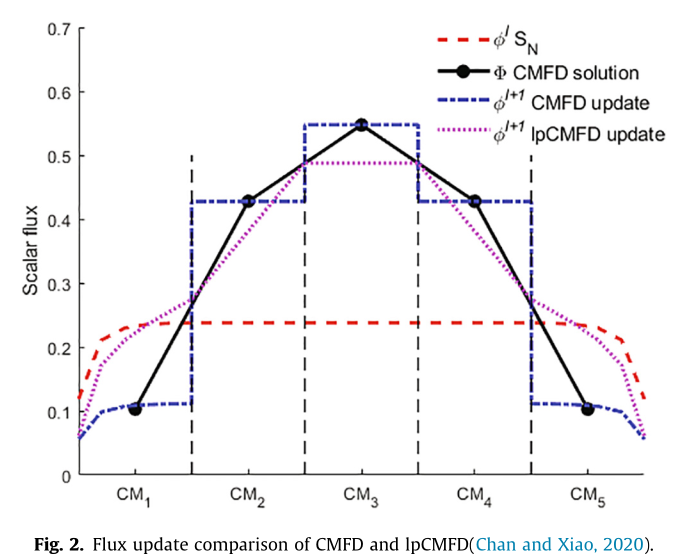
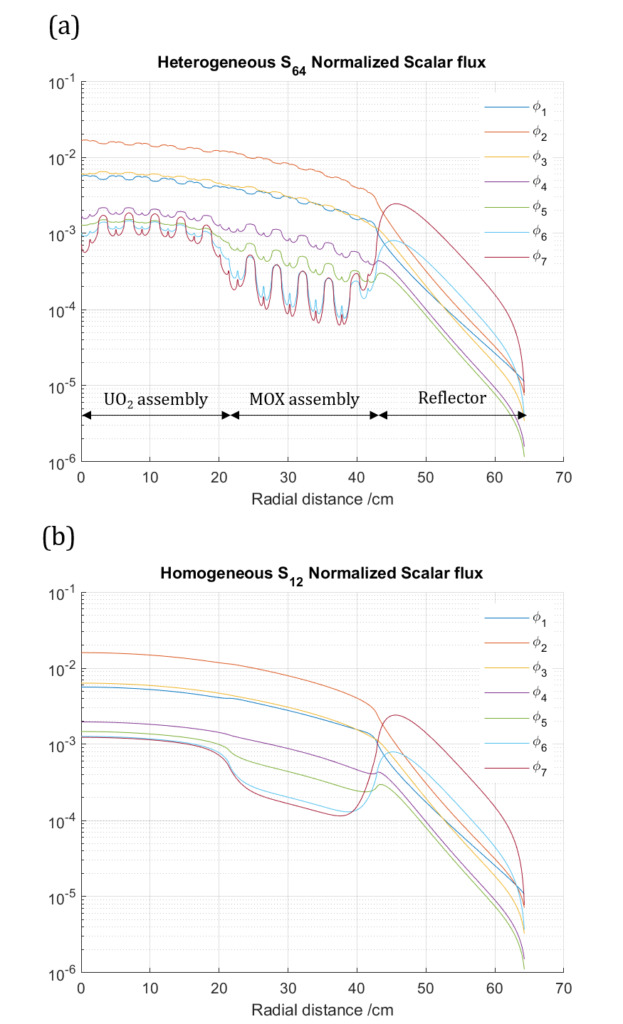
The discrete ordinates neutron transport equation is one of the most exact descriptions of neutron behavior and is employed in state of the art high fidelity neutronic simulations. However, the computational cost of such simulations is high and therefore we commonly employ acceleration schemes. One such scheme is the Coarse Mesh Finite Difference (CMFD) method and its variant, the linear prolongated CMFD (lp-CMFD). lp-CMFD was developed to overcome certain numerical instabilities in CMFD under certain geometrical and cross-section configurations.
Over several papers we extended theoretical analysis of lp-CMFD stability, and tested lp-CMFD on a variety of discretization methods and geometries.

