Introduction
This is an informal summary covering the work which we documented in the following publications:
- Convergence study of CMFD and lpCMFD acceleration schemes for k-eigenvalue neutron transport problems in 2-D Cartesian geometry with Fourier analysis (link)
- Convergence study of variants of CMFD acceleration schemes for fixed source neutron transport problems in 2D Cartesian geometry with Fourier analysis (link).
This is a first part in a multipart series (Parts 2(a), 2(b), 3) where I summarize the work that I performed on lp-CMFD development.
The discrete ordinates ($S_{N}$) neutron transport equation is one of the most accurate ways to simulate the neutronics in a nuclear reactor, but it suffers from requiring a large number of computations and iterations needed for convergence. In the 1960s-1970s, the Coarse Mesh Finite Difference (CMFD) method was developed to accelerate the solution of the neutron transport solution. The basis of the acceleration can be summarized in a non-technical and intuitive way as follows:
- The neutron transport problem sweeps through all the discrete angular directions and only updates the scattering source (and the fission source for a $k$-eigenvalue problem) terms after a pass through all the directions.
- The source term for the first angular flux direction thus has to “wait” until the last angular flux term is solved before being updated at the start of the next iteration cycle.
- The neutron diffusion problem is a less accurate form of the $S_{N}$ neutron transport equation but has much fewer parameters and also fewer computations. Therefore, the solution of the neutron diffusion problem can be used to accelerate the original $S_{N}$ iterations by updating source terms.
- However, because of the approximations made in the neutron diffusion equation, the solution of the neutron diffusion equation may not match up to the real neutron transport solution i.e. the two solutions of the flux and $k_{eff}$ would not converge.
- To fix this issue, we can modify the diffusion drift coefficient to force the two solutions to be identical upon sufficient number of iterations. The drift coefficient effectively modifies the surface current term ($D \frac{d^{2}\phi}{dx^{2}}$) such that it matches the surface current from a transport sweep.
CMFD was wildly successful and is now used is many neutron transport codes such as the NEWT solver in the SCALE package. However, researches quickly realized that the CMFD algorithm had the tendency to become unstable, i.e. the solution does not converge, under certain geometric conditions. Specifically, under conditions when a non-dimensional parameter of the geometry and material cross-section, known as the optical thickness, becomes large. This optical thickness is calculated by taking the cross-section value ($\Sigma$ [1/cm]) and multiplying with the mesh thickness ($\Delta$ [cm]). Due to this behavior, several methods have been proposed to stabilize CMFD. One such method is called the linear prolongated CMFD (lp-CMFD).
lp-CMFD method improvement over CMFD
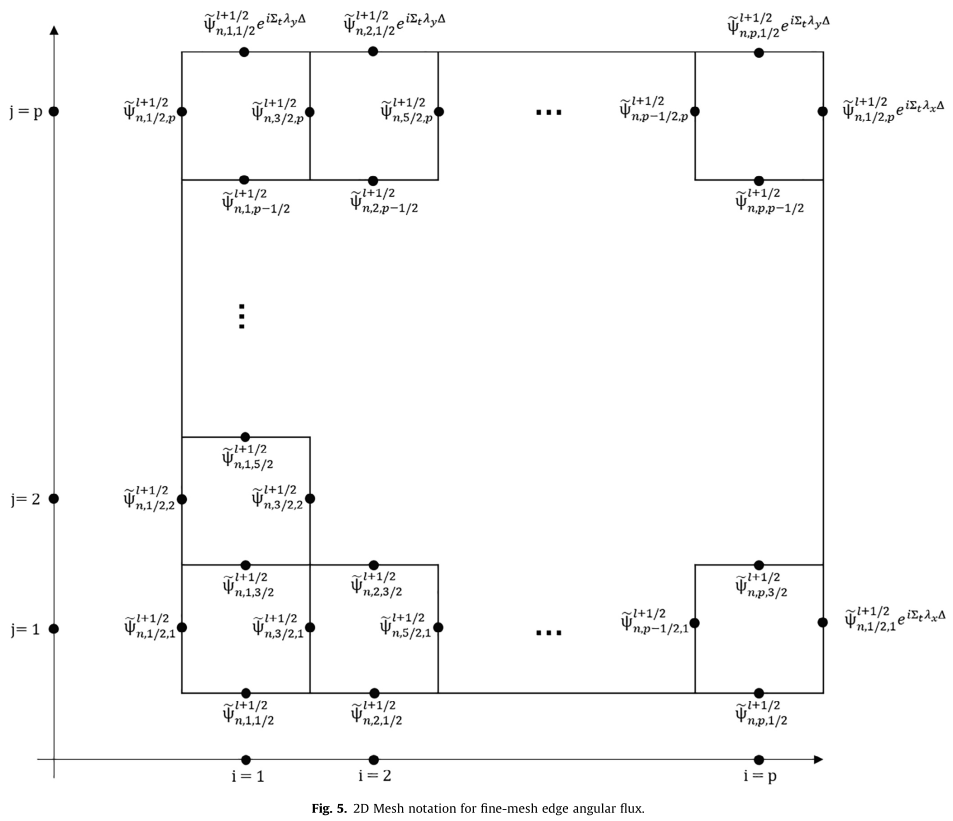
The motivation behind lp-CMFD was to fix a problem that was observed in CMFD during the source term update. CMFD, as the name implies, solves the diffusion equation on a coarse mesh, which is overlayed on top of fine meshes used for the $S_{N}$ neutron transport problem. We shall denote the fine mesh as the variable $m$ and the coarse mesh as $M$. In the step of the algorithm which updates the source term of the $S_{N}$ neutron transport mesh with index $m$, the sources are scaled by a factor $f_{m}$ which is calculated as
$$
f_{m} = \frac{\Phi^{CMFD}_{M}}{\Phi^{S_{N}}_{M}} (m \in M)
$$
we can see that if the CMFD flux ($\Phi^{CMFD}_{M}$) in the coarse mesh is larger than the coarse-mesh averaged flux ($\Phi^{S_{N}}_{M}$), i.e. $\Phi^{CMFD}_{M} > \Phi^{S_{N}}_{M}$, then $f_{m} > 1$ and the source is up-scaled.
One problem with this update method is that all the $f_{m}$ values are identical when they belong in the same mesh $m \in M$. I.e. if coarse mesh $M$ contains fine meshes $m=\{1,2,3,4\}$, then during the update step $f_{1} = f_{2} = f_{3} = f_{4}$. This produces a situation where neighboring fine meshes belonging to different coarse meshes may have large differences in updated source term values despite their physical proximity. This non-smoothness of the update source is one of the reasons why the CMFD iterations becomes unstable at large optical thickness.
The lp-CMFD approach improves upon the CMFD method by using geometric information as an additional input into calculating the update to the source term. Instead of $f_{m}$ as a scale factor, we now calculate a flux update value for fine mesh $m$, denoted as $\delta \phi_{m}$, which is interpolated based on the position of the fine mesh within the coarse mesh (see figure below). $\delta \phi_{m}$ is then used to update the fine mesh flux value by:
$$
\phi^{updated}_{m} = \phi_{m} + \delta\phi_{m}
$$
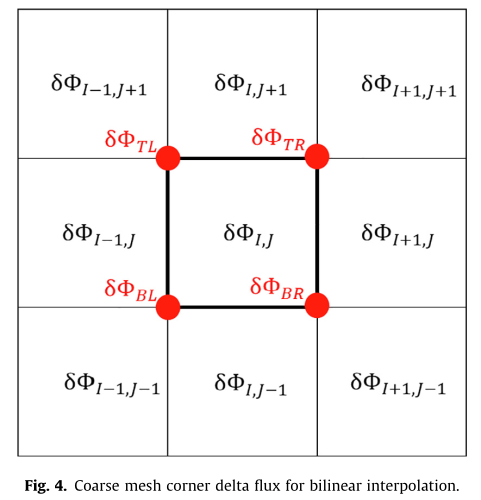
The update flux values for the center mesh are first calculated for the 9 coarse meshes (the 3×3 grid shown above), then calculated at the 4 corner points (indicated by the red dots), and finally calculated using bilinear interpolation for the fine meshes using their position within the coarse mesh.
The upshot of this modification is that the updated fine mesh sources becomes more continuous in relation to neighboring fine meshes and avoids the case where discontinuities appear in neighboring meshes across a coarse mesh boundary.
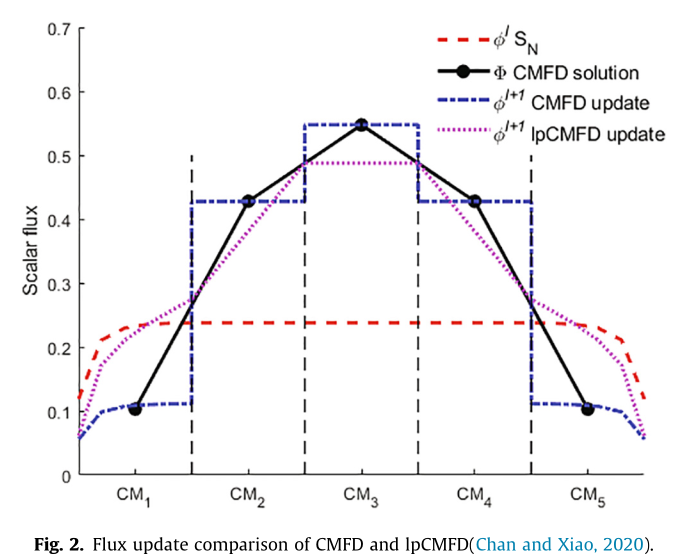
The above figure shows the problem observed for CMFD. The dotted red line shows a single iteration of the flux values from the $S_{N}$ neutron transport sweep. The solid black line shows the coarse mesh diffusion solution $\Phi$. In this case, the entire geometry comprises of 5 coarse meshes with each coarse mesh containing 10 fine meshes. The diffusion equation is solved on the coarse mesh level whereas the $S_{N}$ transport sweep is solved on the fine mesh. The blue dotted line shows the conventional CMFD update.
We can observe that there is a large difference in the updated $\phi_{m}$ in fine meshes which are neighboring each other but belonging to different coarse mesh cells e.g. the sharp discontinuities between $\phi_{10}$ and $\phi_{11}$ which belong to coarse mesh 1 and 2 respectively. This occurs again at $\phi_{20}$ and $\phi_{21}$. We can intuitively grasp that these discontinuities introduces non-physical discontinuities into an otherwise smoothly varying $\phi$ distribution. On the other hand, the lp-CMFD update performs geometric interpolation, which causes the updated flux profile to be more smoothly varying.
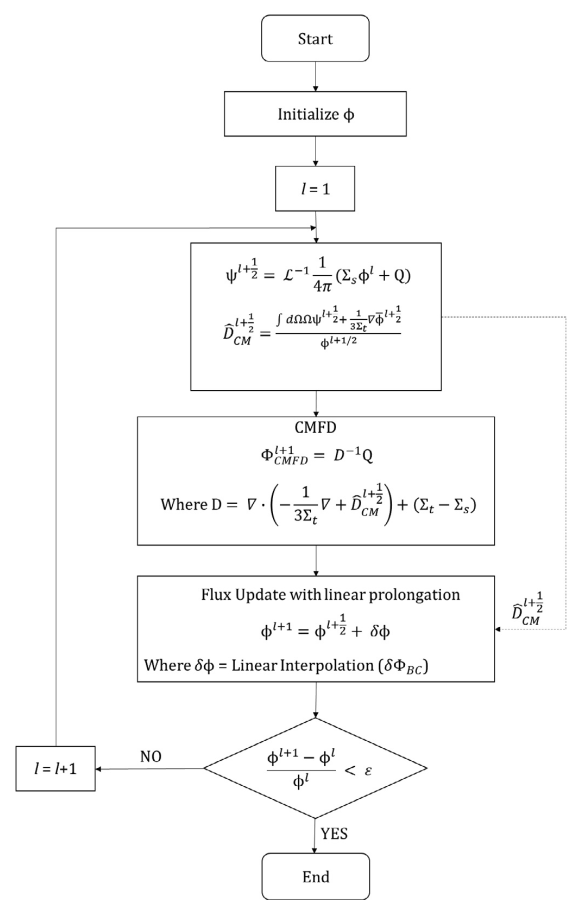
The full lp-CMFD algorithm flow-chart. Not all the steps in the lp-CMFD scheme is explained in this post.
Theoretical Fourier analysis
We performed a convergence analysis on lp-CMFD for 2D geometry for the fixed source and $k$-eigenvalue problem using Fourier analysis. The basis of the method is to first define an analytical solution to the problem with periodic boundary conditions. We then perturb this solution with a small value (a constant ($\epsilon$) multiplied by a periodic function, $\epsilon << 1$). We can think of this perturbation as “noise” over the converged solution.
Intuitively, we can analyse whether this noise parameter becomes larger or smaller on each successive iteration. If it becomes smaller, then we can be confident that the noise will eventually “die away”, and if it becomes larger, we will see that the solution is unable to converge. We therefore define the source noise as $\vec{S}$ and find the error transition matrix $\boldsymbol{M}$ and cast everything in matrix notation:
$$ \vec{S}^{l+1} = \boldsymbol{M}\vec{S}^{l}, $$
where the index $l$ is the iteration index. We can define the spectral radius $\omega$ as the maximum eigenvalue of $\boldsymbol{M}$ and note that if $\omega$ is larger than 1 then the noise term $\vec{S}$ will grow over successive iterations. We are interested in finding the dependence of $\omega$ on the optical thickness of the problem by changing the value of $\Delta \Sigma$ and plotting the resultant value of $\omega(\Delta \Sigma)$.
In addition to the dependence on $\Delta \Sigma$, another parameter which will affect $\omega$ is the scattering ratio, $c$, which is the ratio between the scattering cross-section and the total cross-section.
$$
c = \frac{\Sigma_{s}}{\Sigma_{t}}
$$
Apart from the theoretical spectral radius $\omega$, we also compared numerical values of the spectral radius by implementing our own diamond-difference based $S_{N}$ solver and simulating the periodic problem with additional noise. We can calculate the numerical asymptotic spectral radius which we denote by $\rho$
$$
\rho = \frac{|\phi^{l+1} – \phi^{l}|}{|\phi^{l} – \phi^{l-1}|}.
$$
for large $l$.
That’s a lot of math, so let’s check out some of the figures! The figure below shows $\omega$ profile against $\Delta \Sigma$ for different CMFD variants for the fixed source problem for $c=0.6$.
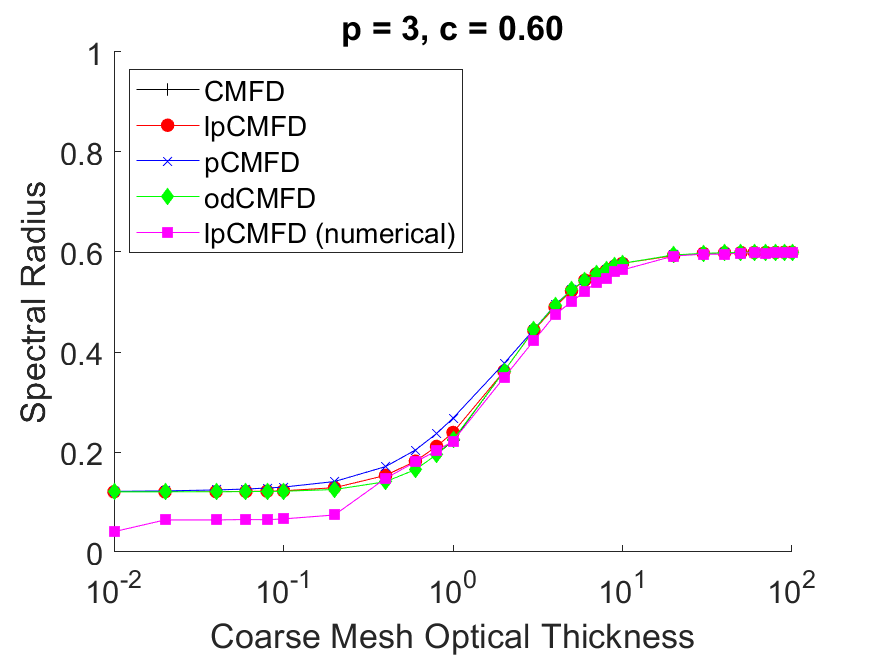
We can see that $\omega$ is less than 1, which shows that all the CMFD variants will converge in this configuration. We also observe that low values of $\Delta \Sigma$ will also lead to low values of $\omega$. This is important as it shows that low values of $\Delta \Sigma$ will lead to faster convergence using CMFD and CMFD will not be as effective as an acceleration technique at high $\Delta \Sigma$.
Now we will observe what happens when we increase the scattering ratio from $c=0.6$ to $c=0.99$
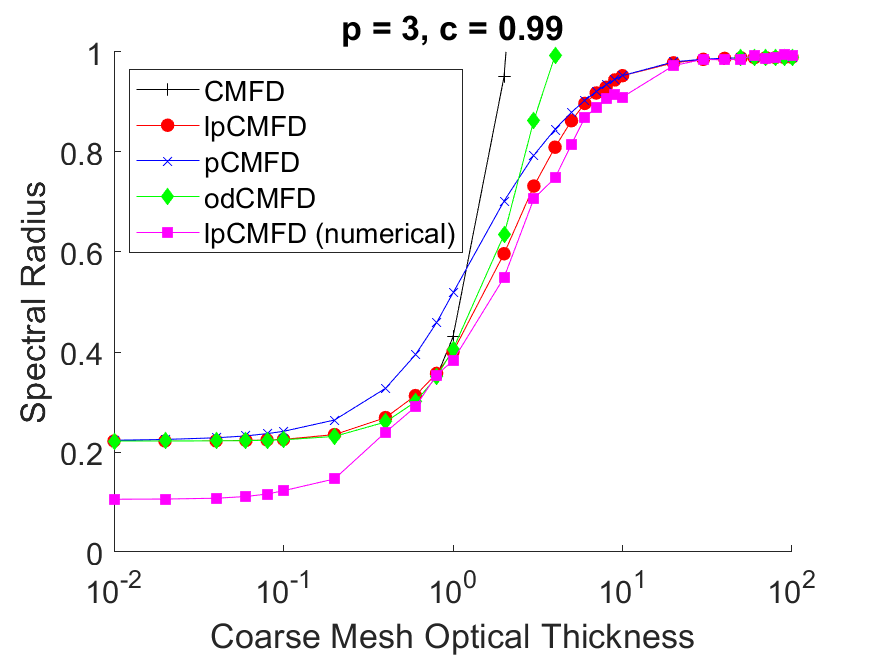
We can observe that for this case the CMFD method (indicated by the black line) diverges ($\omega > 1$) at high coarse mesh optical thickness, whereas lp-CMFD and some of the other CMFD variants remain stable. Another thing to observe is that all the CMFD variants have much larger values of $\omega$ in general at high $\Delta \Sigma$ for $c=0.99$ compared to $c=0.6$. Again, high $\omega$ values are indicative that the acceleration method becomes less effective.
In summary…
The two publications in this work furthered the theoretical analysis of lp-CMFD to 2D geometries. We showed this by performing a Fourier Analysis for different CMFD variants. We also showed the dependence of the spectral radius on several different geomety parameters. The results for 2D geometries largely agree with the theoretical analysis performed for 1D geometries.