Introduction
This post is an informal summary of the paper “A linear prolongation CMFD acceleration for two-dimensional discrete ordinate k-eigenvalue neutron transport calculation with pin-resolved mesh using discontinuous Galerkin Finite Element Method” published in Annals of Nuclear Energy in May 2021. This is a part 2(b) in a multipart series (Part 1, 2(a) and 3) where I go through the work I performed on lp-CMFD extension and testing.
In part 2(a) we covered the extension of lp-CMFD to the DGFEM discretized form of the $S_{N}$ neutron transport equation in 1D geometries. In this post we will cover the work that we did and numerical testing for 2D geometries. This demonstration is much more useful for practical neutron transport problems.
DGFEM basis functions for 3 and 4 sided polygons
The 1D basis functions which we used in Part 2(a) was the Lagrangian and Legendre basis functions. These sets have their equivalent sets in 2D spaces1. For 3 and 4 sided polygons we have the following Lagrangian points denoted by black dots.
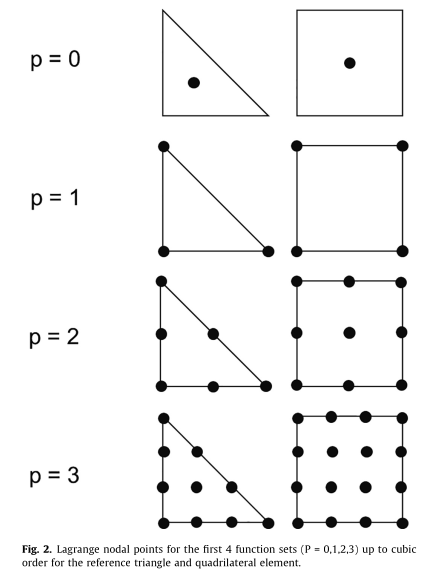
The corresponding Lagrangian points in 2D for triangle and square meshes. Note that the dots represent points where the Lagrangian basis set outputs 1. Also note that triangular and square meshes can be skewed, transformed or rotated with appropriate normalization methods.
The flexibility of 2D DGFEM allows for semi-structured and unstructured meshes, which is able to model the pin-structures in a PWR assembly.
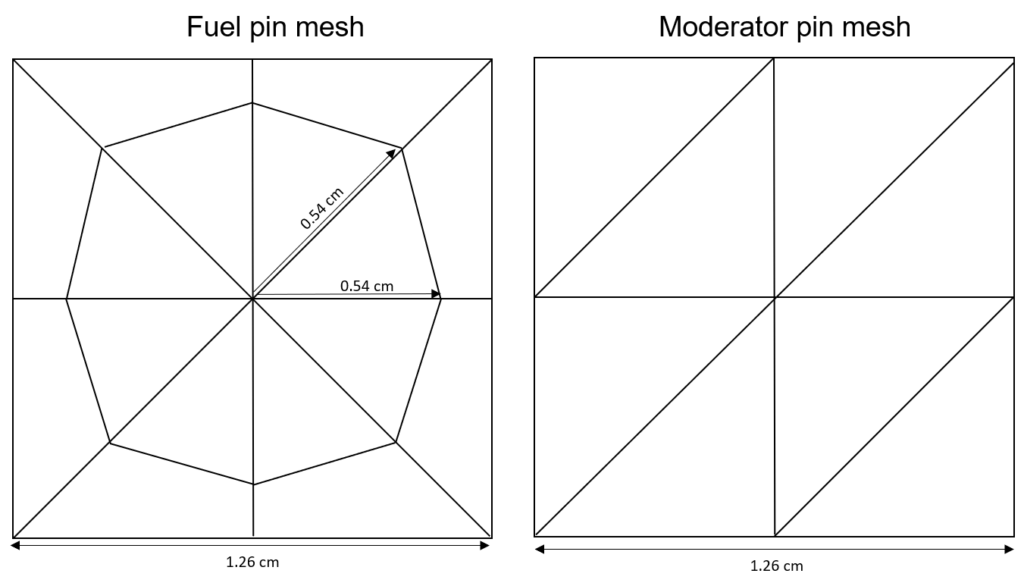
and we can connect these meshes arbitrarily and even have different basis function set polynomial orders in neighboring meshes.
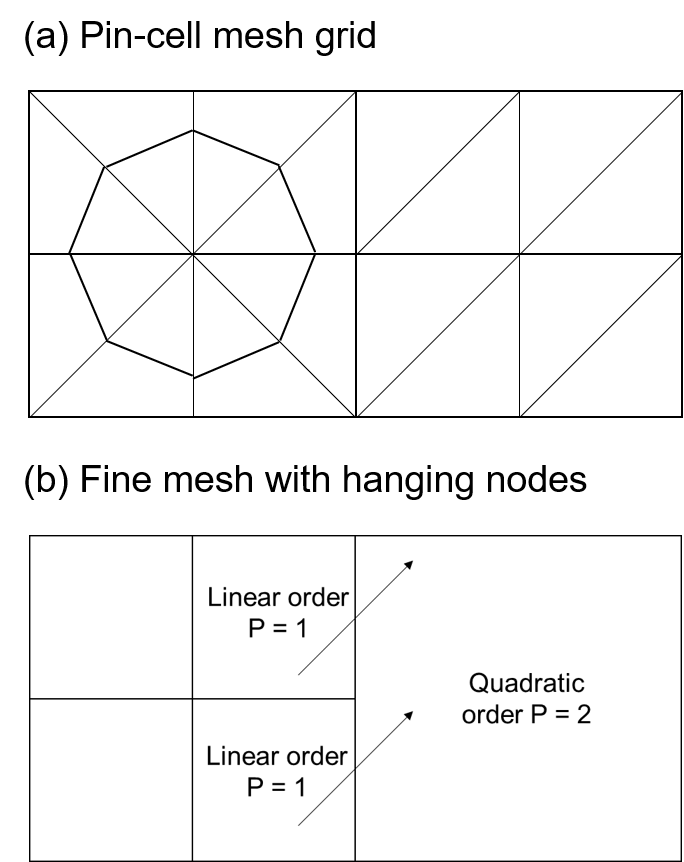
A major portion of this work was coding my own DGFEM solver for the $S_{N}$ neutron transport equation. We did not have access to any preexisting code for this purpose so we had to start from scratch.
lp-CMFD update
In order to update the coefficients for the basis functions in each fine mesh, we needed some way to perform interior interpolation of the update values in the coarse mesh. For rectangular meshes, this is done with bilinear interpolation on the coarse mesh vertices, and we implemented a Barycentric interpolation method for general convex polygons which we wrote about in Part 3.
Let us denote the interpolation function as $f(\vec{r})$ dependent on the coordinates inside the coarse mesh $\vec{r}$. We can define the update coefficients vector as $\vec{s}$ with $I$ number of components. The update profile on the fine mesh is define on the same basis function set as for the $S_{N}$ transport
$$
g(\vec{r}) = \sum^{I} s_{i}u_{i}
$$
where $u_{i}$ is the functions within the basis function set $u = \{ u_{0}, u_{1}, … u_{I}\}$
The DGFEM method of weighted residuals provides us with $I$ number of equations by multiplying $g(\vec{r}) – f(\vec{r})$ with basis function $u_{i}(\vec{r})$ and integrating over the fine mesh domain i.e.
$$
\int (g(\vec{r}) – f(\vec{r})) \cdot u_{i}(\vec{r}) dr = 0
$$
clubbing together all $I$ equations gives as $I$ simultaneous equations which can be expressed in matrix notation as
$$
\boldsymbol{T}\vec{s} = \vec{v}
$$
which we can solve
$$
\vec{s} = \boldsymbol{T}^{-1}\vec{v}
$$
Note that the matrix $\boldsymbol{T}$ has already been pre-calculated for the DGFEM calculation for the $S_{N}$ transport calculation.
Numerical tests
We conducted two numerical tests using the 2D C5G7 problem and a hexagonal problem.
2D C5G7 multigroup problem
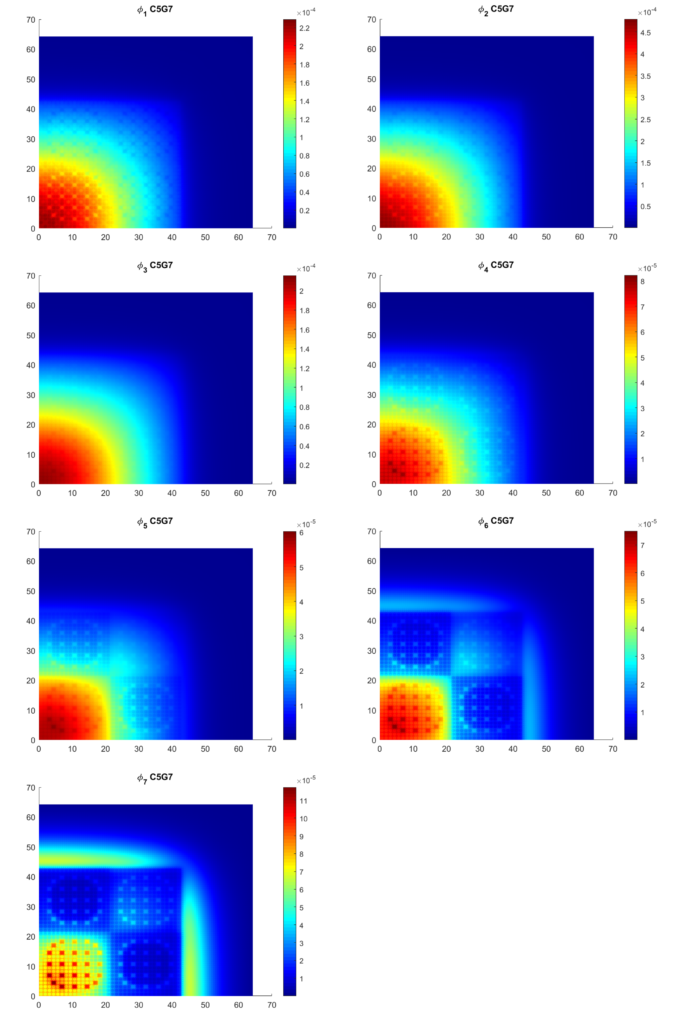
The geometry of the C5G7 problem2 consists of a quarter core model with 2 different types of assemblies. We define the coarse mesh for this problem over each assembly.

The C5G7 problem has 7 energy groups and the flux solutions for this problem are shown in the following figures.
The comparison between various CMFD variants are shown in the following figure. We also varied the maximum polynomial order $P$ for the fine mesh basis functions from 0 – 3.
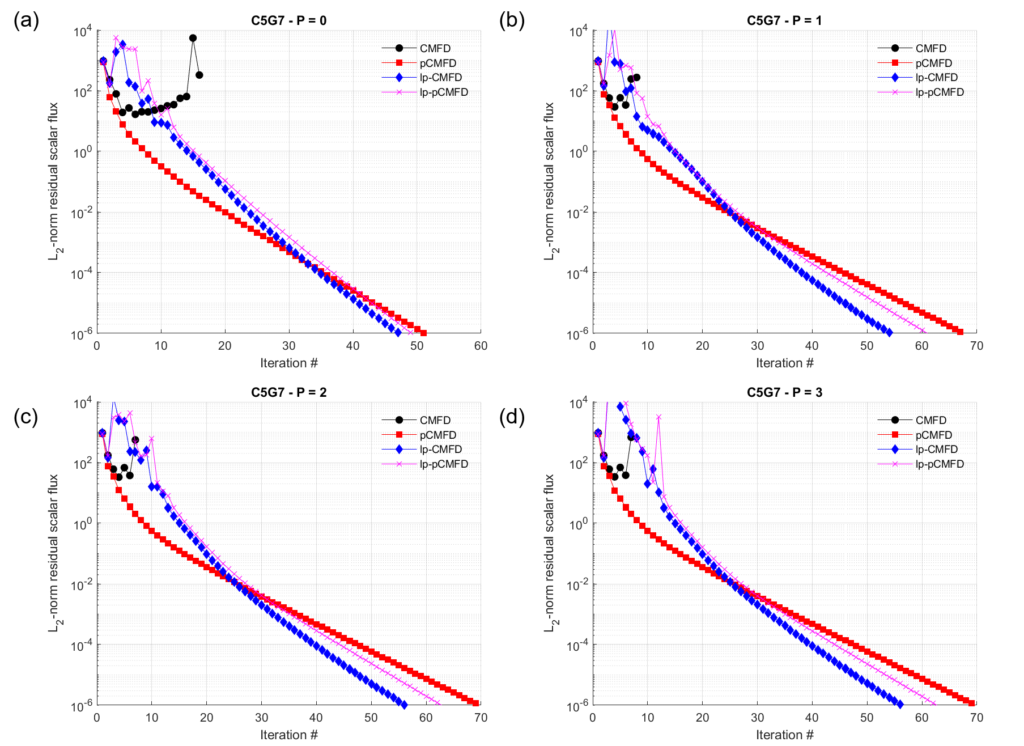
We can see that CMFD diverges whereas the other acceleration schemes are stable. The lp-CMFD scheme has the best performance for this problem out of lp-pCMFD and the pCMFD methods.
Hexagonal geometry
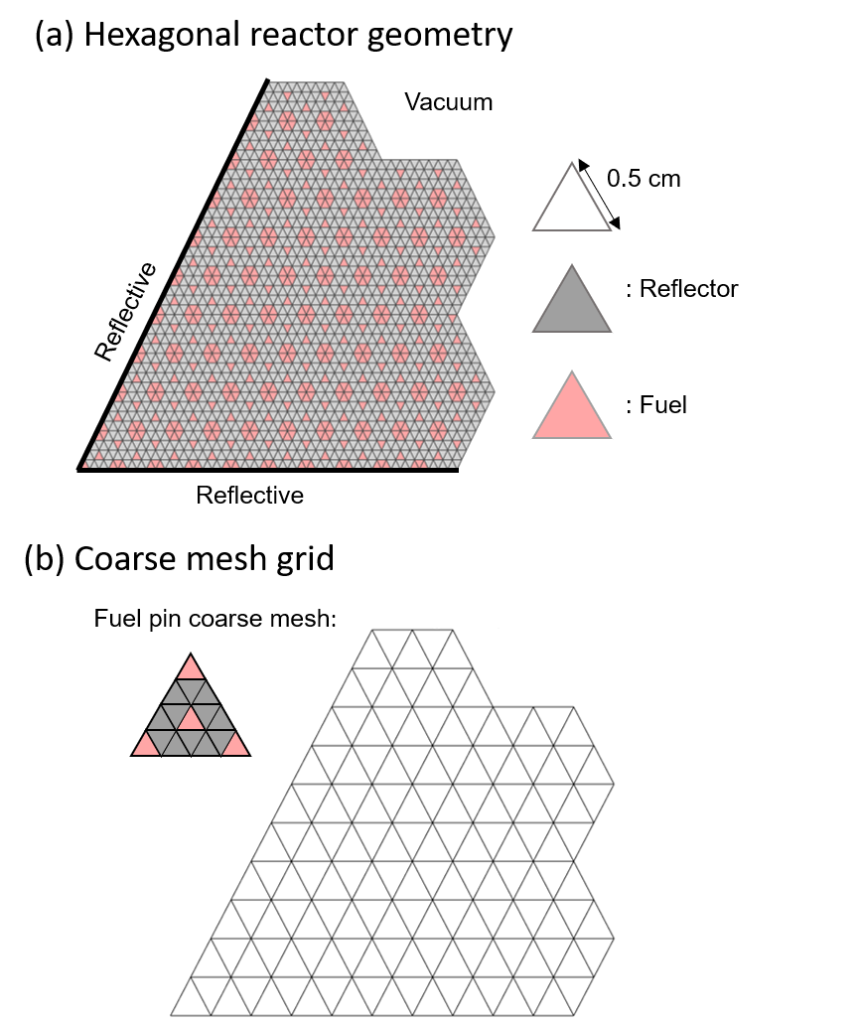
We next tested using a hexagonal reactor model. The geometry is shown below:
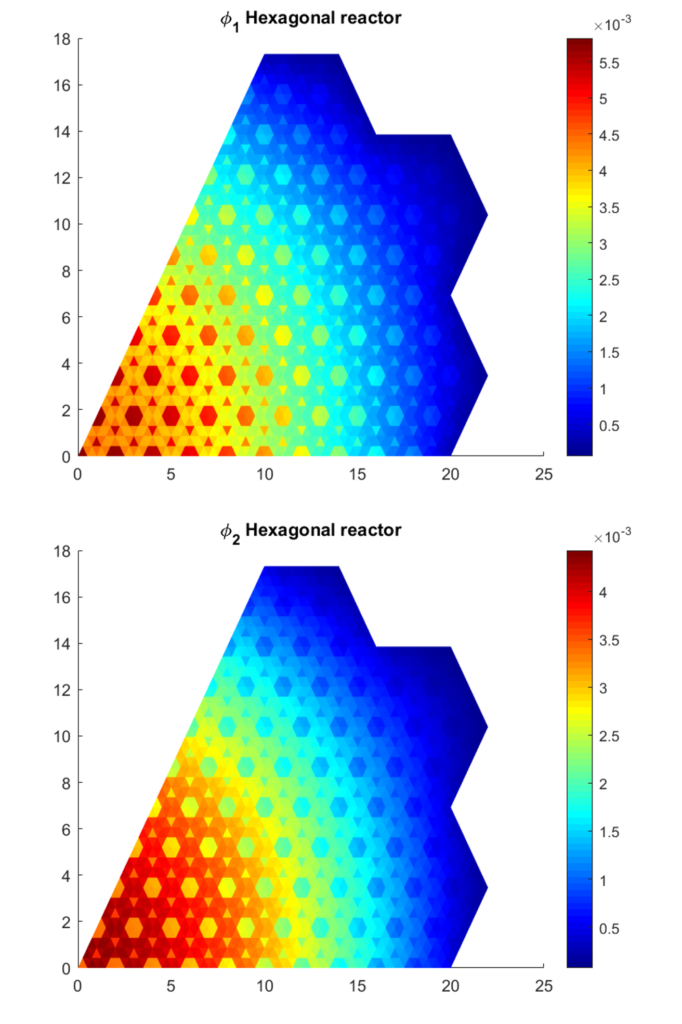
The 2-group flux solutions are shown below.
And the results of the acceleration comparisons are shown below.
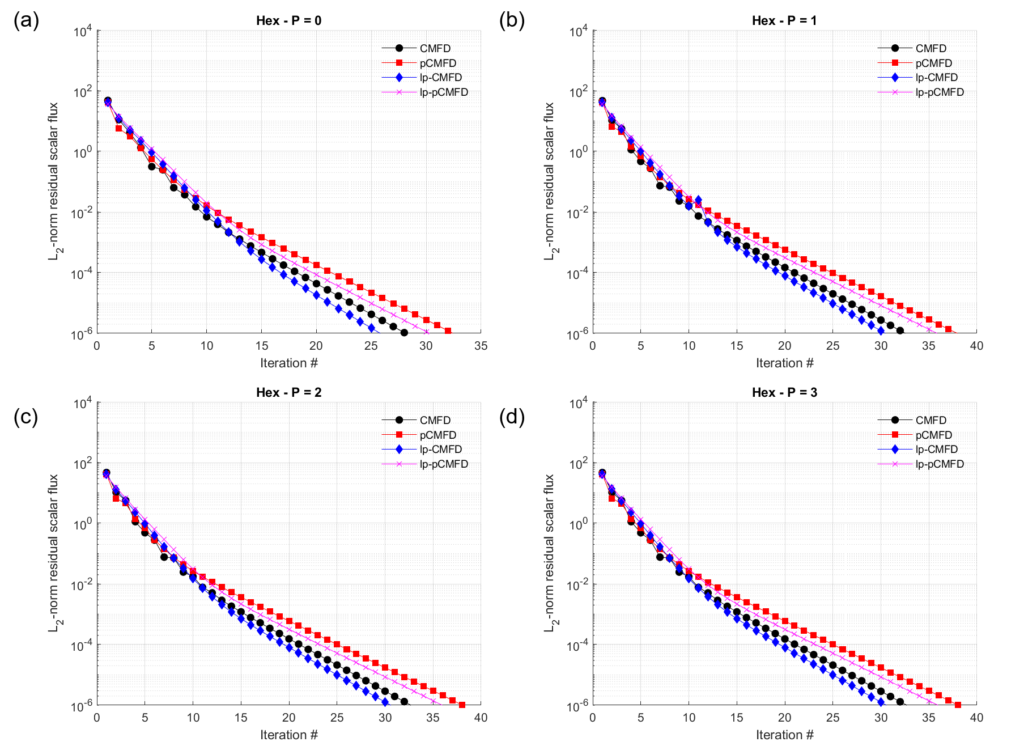
For this benchmark problem, CMFD is able to converge, however its performance is slightly worse than lp-CMFD.
In summary…
This post is slightly shorter since it was really a numerical study demonstrating the effectiveness of lp-CMFD for a variety of realistic 2D reactor geometries. We extended the earlier 1D DGFEM implementation to 2D DGFEM implementation, combining our work on Barycentric coordinate systems to update non-rectangular geometries which is covered in Part 3. Overall, lp-CMFD was shown to be stable and had the best performance out of the CMFD variants tested. I hope you liked the colorful graphs of the flux solution and the geometries which I spent a long time developing the code for!
Footnotes
- The theory and methodology of DGFEM to 2D neutron transport problems can be found in two sources which I used extensively:
Y Wang and J.C. Ragusa, “A high-order discontinuous Galerkin method for the SN transport equations on 2D unstructured triangular meshes”, Annals of Nuclear Energy Vol 36, (2009)
Y Wang “Adaptive mesh refinement solution techniques for the multigroup SN transport equation using a higher-order discontinuous finite element method”. PhD. dissertation. (2009) ↩︎ - OECD/NEA “Benchmark on Deterministic Transport Calculations Without Spatial Homogenisation” (2003) ↩︎

