Introduction
This post is an informal summary of the work we did to expand and improve MAREN, the details of which we published under “Representation of multi-group cross section libraries and flux spectra for PWR materials with deep neural networks for lattice calculations”1 in Annals of Nuclear Energy in December 2024 (open access here). It is recommended to read the first paper summary post establishing MAREN, which can be found here. This paper does not introduce any new machine learning techniques unlike in the earlier post but rather focuses more on expanding the model using the same machine learning techniques (Principal Component Analysis (PCA) + Deep Neural Network (DNN) methods).
Recap of MAREN…
In an earlier post, we presented a first-of-a-kind regression model (MAREN: MAchine learning based REpresentation for Nuclide cross-sections) which takes in the following inputs…
- Nuclide vector of the fuel pin ($N$ [atoms/b-cm])
- Fuel pin temperature ($T_{f}$ [K])
- Moderator temperature ($T_{m}$ [K])
- Moderator density ($\rho$ [g/cm3])
- Dissolved boron concentration ($B$ [ppm])
… and outputs the multi-group cross-section (MGXS) libraries for the fuel pellet material found in typical PWR assembly designs.
The MGXS library had 56 energy groups for 38 nuclides (37 real nuclides and a fictitious “BASE” cross-section). We showed that a combination of PCA dimensionality regression and DNN mapping was able to map ~10s of input parameters to ~1000s of output parameters which comprise the MGXS library.
After the original paper was published, in the following months we optimised MAREN by playing around with the input parameter space and also expanded MAREN capabilities in several notable ways.
Improvements and optimisations
The major differences between the previous version of MAREN and the updated version is shown in the following Table.
| Old MAREN | New MAREN | |
| Material libraries modeled | Fuel pellet only | Fuel pellet Zircalloy cladding He gap Borated water B4C control rod Stainless steel Air |
| # of nuclide libraries generated in fuel pellet | 37 | 86 |
| Nuclides in input space | 37 | U + Pu isotopes (7 species) |
| Arbitrary flux-weighted collapse | Not possible because representative 56-group flux not one of the model outputs. | 56-group flux in fuel and moderator materials predicted based on input parameters. Allows for arbitrary flux-weighted collapse of MGXS libraries into FGXS libraries |
1. Material XS libraries modeled
The first MAREN paper focused on predicting the MGXS libraries for the fuel pellet material. We realized that for MAREN to be usable in assembly lattice calculations it needed to also predict the MGXS libraries for other common materials used in PWR assemblies. These materials can be divided according to several pin types found in the reactor which are the fuel pin, the instrumentation tube and the control rod.
We used the pin geometries from the MIT BEAVRS benchmark. In total our new MAREN model has to predict the MGXS library for 7 materials compared to 1 material from the earlier version.
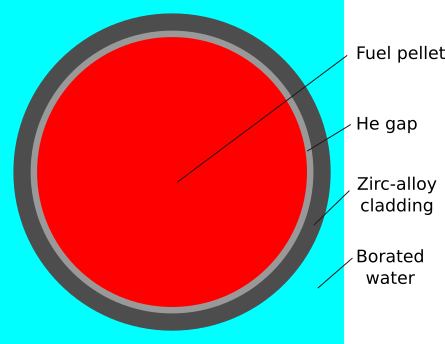
The fuel pin contains the fissile material, and comprises of the following layers, starting from the center:
- The fuel pellet made of UO2
- A gap of pressured helium
- Cladding made of Zircalloy
- Surrounding the fuel pin is borated water, i.e. ordinary water with dissolved boron at ~100s of ppm concentration
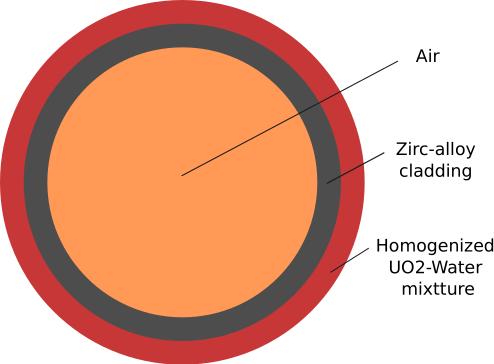
The instrumentation tube, as the name suggests, is a channel through which various detectors can be used to monitor the core. The innermost cylinder is filled with air.
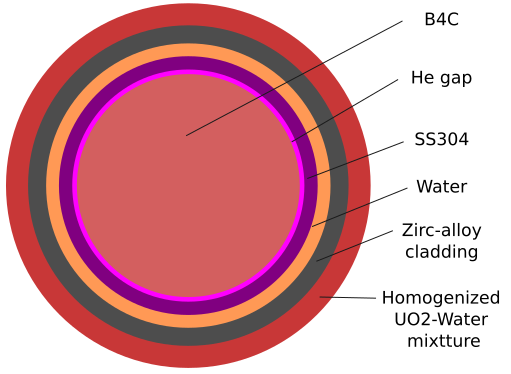
The control rod is used to absorb neutrons and is used to control the reactivity of the core. It comprises of the following additional materials:
- B4C, a highly neutron absorbing material
- Stainless steel SS304, used as cladding for the control rod
The mean value (represented by blue bars) and standard deviations (represented error bars) of the fuel pellet macroscopic fission in the test data is shown below. The variation in the MGXS is due to variations in the input parameter space.
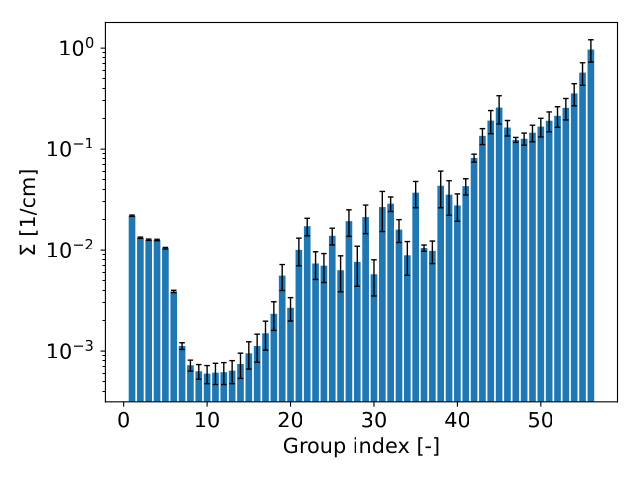
The fission MGXS has very low values at the fast energy range ($g \leq 10$) but increases rapidly in the thermal energy range ($g \geq 40$ i.e. at 0.0625 eV). Note that the y-scale is logarithmic. The next figure shows the fuel pellet total XS:
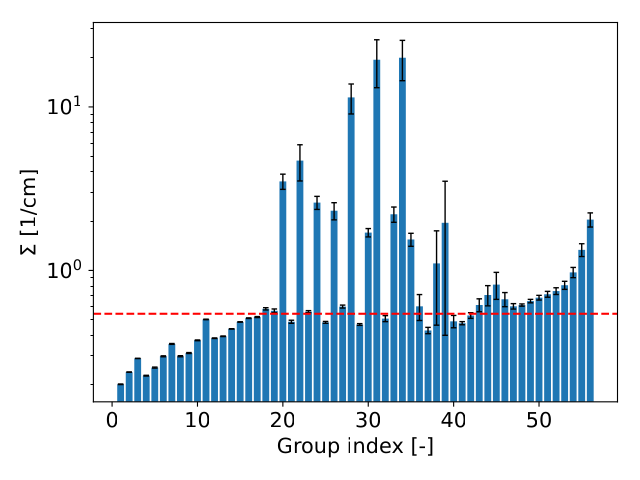
The total MGXS is characterized by a “background” value of 0.543 barns (with the dotted red-line), with a handful of peaks between groups 20 and 35, which are due to resonance absorption from U isotopes. These few spikes causes a corresponding depression in the fuel pellet flux distributions for these energy groups, which we will see later.
Another thing we should note that is the fact that the largest variations occur only in a small number of groups. For example, compare the large variance for group 39 with the the small variances for XS in the fast energy range ($g \leq 20$). We take advantage of this fact by using PCA to identify components with the largest variations up to some threshold and to map the the value of the coefficients associated with this component on the input parameters.
Lastly we will show the total cross-section for borated water.
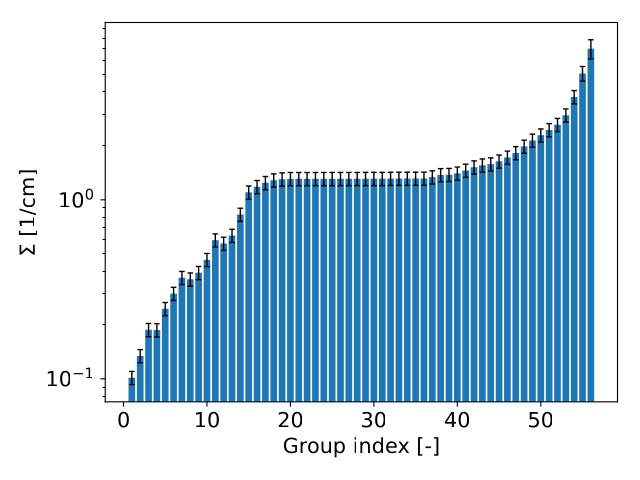
The total XS profile for borated water is much simpler than the fuel pellet. The XS starts small at low $g$ values and increases exponentially at high $g$ values.
2. # of nuclide libraries generated for fuel pellet
Our initial MAREN model generated microscopic cross-section libraries for 37 nuclides together with a “BASE” cross-section. For more accurate fuel pellet macroscopic cross-sections, we can expand the # of nuclide libraries so that we can more accurately reconstruct the fuel pellet macroscopic cross-sections.
The list of nuclides which we selected was modified from the SCALE default list, which is optimized for PWR calculations. Our final list comprises of 86 isotopes which are shown in following table. Another advantage of this approach is that now we can predict the MGXS libraries for fuel pins with different densities as well.

3. Nuclides species in input space
The original MAREN used the concentrations of 37 nuclides as the input parameters . Over the next few months we extensively tested various combinations of nuclide isotopes which make up the nuclide vector as input parameters. Ultimately, we found that using only the uranium and plutonium isotopes’ concentrations as inputs parameters produced equally good regression results compared to the complete nuclide list. These species are: $U^{234}$, $U^{235}$, $U^{236}$, $U^{238}$, $Pu^{238}$, $Pu^{239}$, $Pu^{240}$, $Pu^{241}$ and $Pu^{242}$. Because we reduced the length of the nuclide vector, we decided to drop the PCA dimensionality reduction step for the nuclide vector.
4. Arbitrary flux-weighted collapse
MAREN generated MGXS libraries contain 56-energy groups with the group structure found in the SCALE code package. For different applications, it would be useful to be able to perform flux-weighted collapse into fewer energy groups. The flux-weighted procedure calculation is
$$
\sigma_{G} = \frac{ \sum{ \sigma_{g} \phi_{g} } } { \sum \phi_{g} } \text{ for } g \in G ,
$$
where $g$ is the index of the fine energy group (between 1 and 56) and $G$ is the larger coarse energy group. E.g. if $G_{1}$ contains $g_{1}, g_{2}, g_{3}$, then the XS for $G_{1}$ is
$$
\sigma_{G_{1}} = \frac{1}{\phi_{1} + \phi_{2} + \phi_{3}} (\sigma_{1}\phi_{1} + \sigma_{2}\phi_{2} + \sigma_{3}\phi_{3}).
$$
Flux weighted collapse is only possible if we have representative flux values $\phi_{g}$ for the 56 energy groups. These representative flux values are also dependent on nuclide vector in the fuel pellet and the state parameters of our assembly, and so we also expanded MAREN to predict the fuel flux based on these input parameters.
The fuel pellet flux values can be used to perform flux-weighted collapse for the fuel pellet material MGXS library, however for the other materials (e.g. borated water, zircalloy cladding etc.), a more accurate representative flux is needed to collapse the MGXS libraries. Therefore, we also trained MAREN to generate the flux distribution found in the borated water.
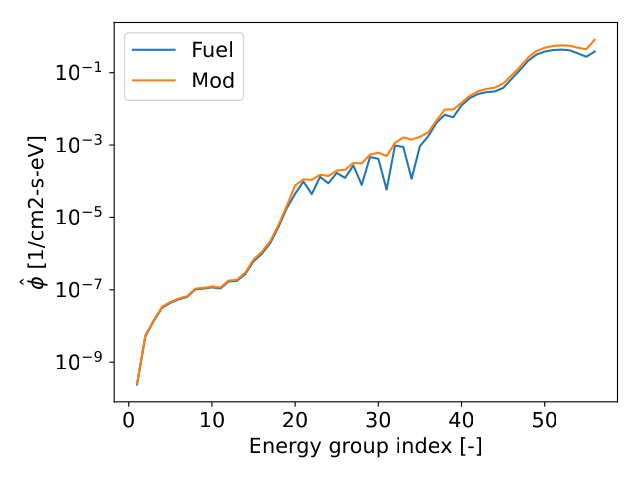
This figure shows the average flux profiles in the fuel and the moderator, which are roughly similar. The fuel pellet flux has a few ‘dips’ between energy groups 20 – 35 as a result of increased absorption due to resonance peaks from U isotopes.
Interestingly, on testing MAREN, we found that the error in the predicted fuel flux was larger than the moderator flux as shown in the figure below. The fuel flux had around 1-2% relative error while the moderator flux had around 0.3-0.4% relative error. This is probably due to the fact that the fuel flux is much more sensitive to the fuel pellet nuclide vector and the assembly state parameters.
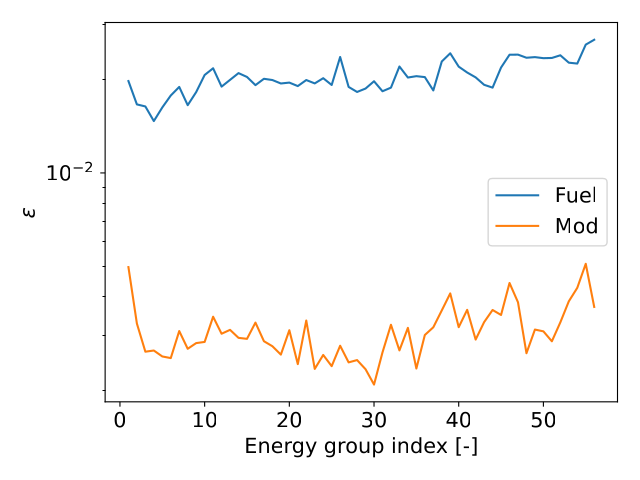
The relative error value $\epsilon$ above is calculated as $ \frac{|y – y^{ref}|}{ y^{ref} } $.
Results analysis
We performed an error analysis of our new MAREN model in two ways:
- Direct comparison of 56-group MGXS libraries with reference libraries
- Input MAREN MGXS and reference MGXS into a transport code and compare $k_{eff}$ and pin power distribution errors
- Use flux-weighting to convert MGXS into FGXS libraries and perform the same $k_{eff}$ and pin power error analysis
Direct comparison of MAREN MGXS and reference MGXS
Overall, we found that MAREN was able to accurately predict the values of the various materials’ MGXS libraries. The largest errors are to be found in the fuel pellet and borated water materials due to the fact that these materials are most strongly affected by variations in the input parameters. The relative errors are still highly accurate and the mean relative error is <1%.
Error analysis for fuel pellet fission and total XS
$\epsilon$ for fuel pellet fission XS across 56 groups are shown in the following figure
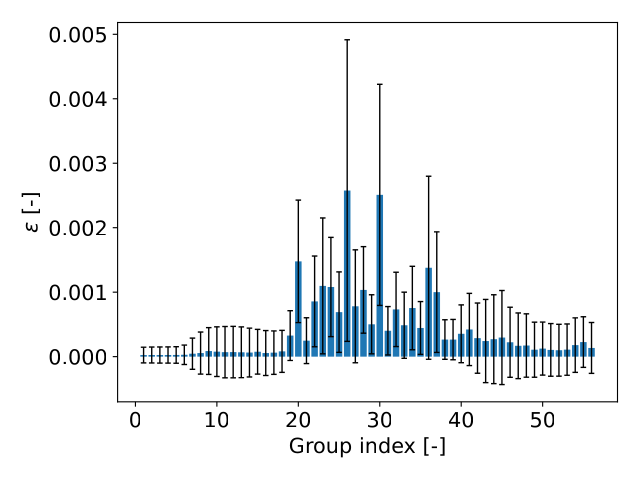
The relative error values are less than 1% and the errors are not uniform. The errors are largest and with the highest variance (indicated by the error bars) between groups 20 and 35. This is due to the fact that these groups’ fission XS values show the most sensitivity to the input parameters (again due to resonance effects!).
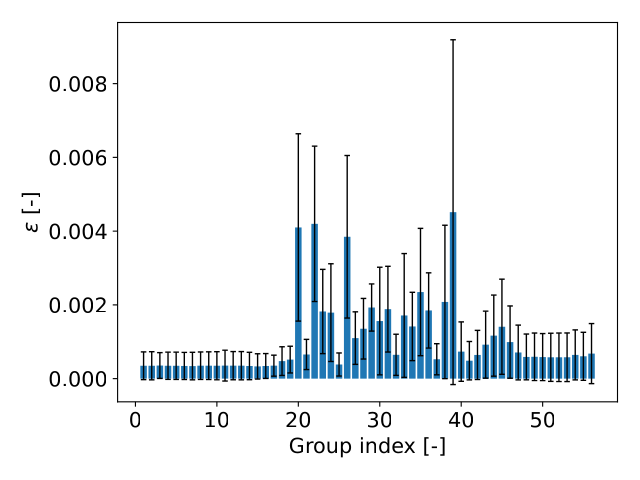
The same phenomenon occurs for the total XS as shown above, where the errors are concentrated between groups 20-35.
Error analysis for the borated water total XS
The $\epsilon$ values for the borated water total XS is shown below.
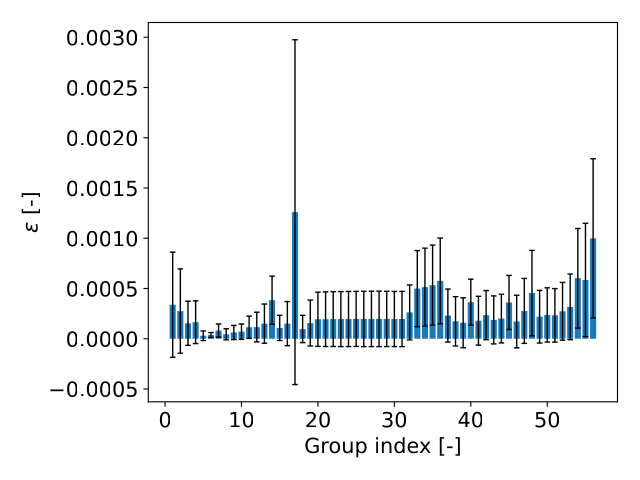
The $\epsilon$ values for the borated water total XS is much more uniformly distributed than for the fuel pellet.
Total XS error analysis for the other assembly materials
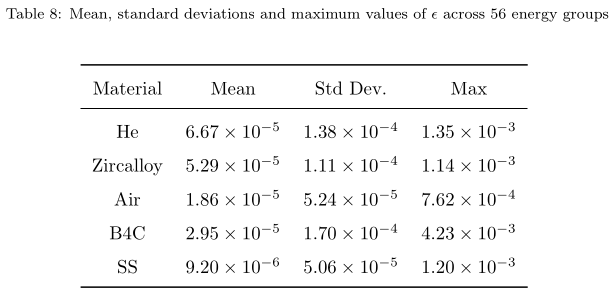
MAREN generates the MGXS libraries for the other materials at much higher accuracy than for the fuel pellet and the borated water with mean values of $\epsilon$ around $10^{-5}$-$10^{-6}$.
Comparison of MAREN MGXS on typical assembly lattice models
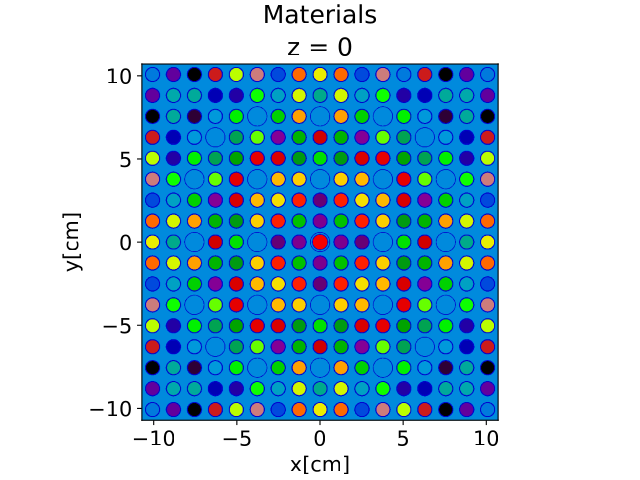
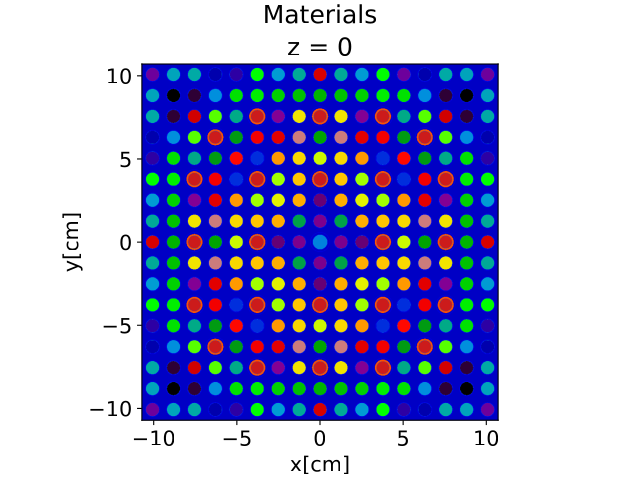
We ran two sets of lattice calculations with MGXS libraries. The first set is from MAREN generated MGXS libraries predicted from test input data and the second set is the reference generated MGXS libraries from the test inputs. We then compared the $k_{eff}$ value and the pin power distribution. The two figures show the configuration of the assembly lattice without control rods (top) and with control rods (bottom), the instrumentation tube is at the center of the 17×17 assembly.
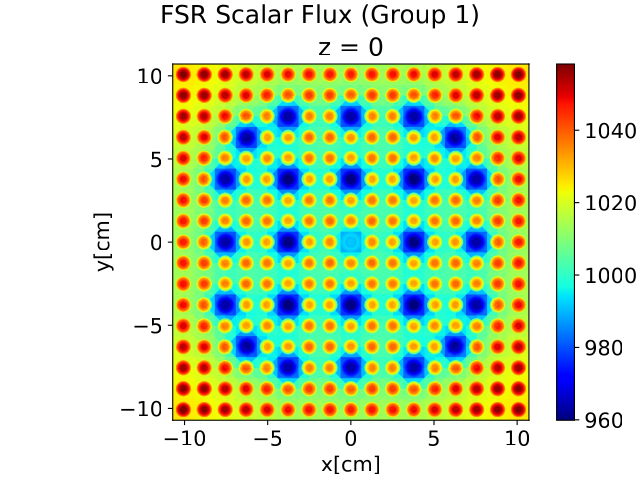
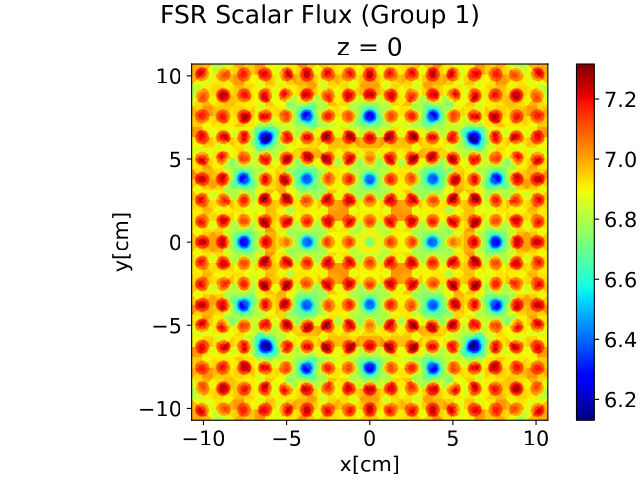
The next two figures show examples of the fast group scalar flux for the model without control rods (top) and with control rods (bottom). The fast group scalar flux is indicative of the fission sources, because fission is the source of the fast flux. For the model without control rods, the pin positions are marked in red and the pin positions filled with borated water are in blue.
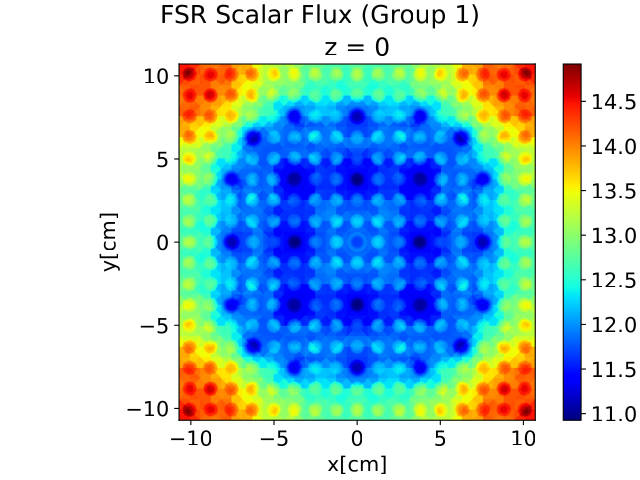
For the assembly model with control rods inserted, we can see that the fast flux is now concentrated in the corners of the model as the control rods greatly reduce the neutron distribution in the center of the reactor. This causes the corner fuel pins to have the majority of the fission distribution in the assembly.
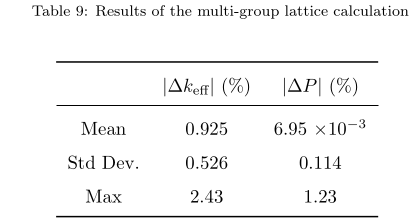
The error for the $k_{eff}$ value and the pin power distribution is shown in the following table.
Comparison of MAREN FGXS on typical assembly lattice models
One of the main features of the updated MAREN model is to generate FGXS libraries using the flux-weighting method. This is carried out by first generating 56-group MGXS libraries and 56-group reference fluxes based on the input values and finally calculating the FGXS using the flux-weighting equation. We used this method to produce 2-group FGXS libraries and re-performed the lattice calculations with only 2 groups (“Fast” and “Thermal”). The typical spatial distribution of the fast and thermal fluxes for the assembly without control rods inserted are shown in the figures below.
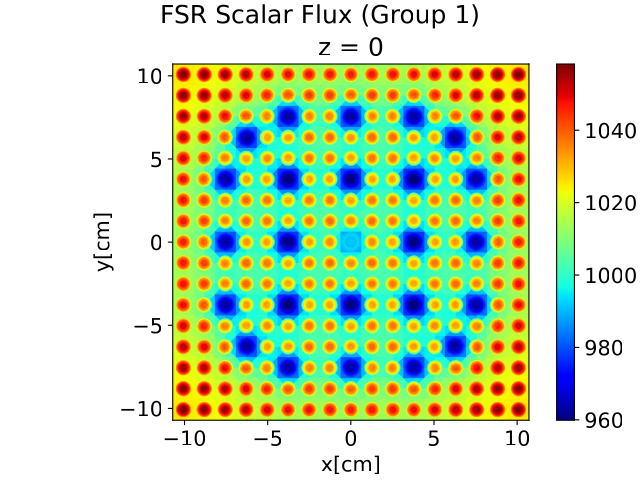
The spatial distribution of the fast flux ($g$ = 1). As before, the red zones represent regions where the fast flux is highest. The blue regions is the located of the water channels, which have the lowest amount of fast flux because neutrons in those regions slow down to the thermal flux. Also interesting to note is that the corner fuel pins exhibit the highest rate of fission. This might strike PWR assembly design engineers as strange because typically it is the fuel pins nearest the water channels that will have the highest fast flux because thermal neutrons from the water channels would escape and cause fission on the surrounding fuel pins. This strange behavior is explained by the fact that the water channels have significant levels of boron, which acts as a neutron absorber and therefore prevents the thermalized neutrons from escaping the water channel.
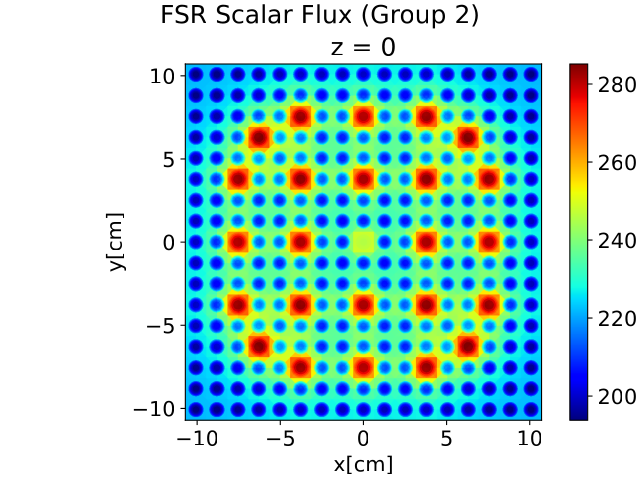
The spatial distribution of the thermal flux ($g$ = 2). The red zones represent the water channels, where fast neutrons generated from the surrounding fuel pins interact with water and down-scatter to thermal neutrons.
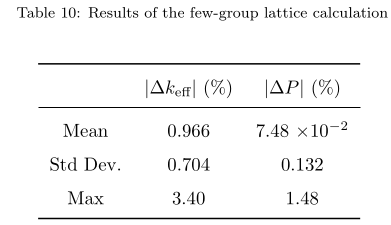
The few group lattice calculation results are similar to the multi-group lattice calculation results, with $k_{eff}$ <1% error.
Github repository
In an effort to make the results of this work accessible, I created a public Github repository for MAREN. This streamlined MAREN model (trained with Tensorflow and designed to be used with python API) contains only the trained model weights and normalization parameters and excludes the various training routines and pre-processing used to train the model. We created this as a convenient tool for engineers, teachers or scientists who want to use MAREN for applications but cannot train such a large regression model themselves. The project can be found at this link. Hopefully I can find the time to update the repository with more examples or to even post a step-by-step example here as post in the future.
In summary…
The PCA + DNN method established in the previous paper was an effective method of predicting high dimensional MGXS libraries based on large input parameter space. In this paper we expanded MAREN by applying the same method onto many more assembly materials, more nuclide microscopic MGXS libraries and the flux spectra distributions. We then conducted error analysis and found that (1) the generated MGXS libraries were accurate with relative errors <1% and (2) typical assembly lattice calculations using these predicted MGXS libraries produce $k_{eff}$ errors of <1%. MAREN can now be used to simulate a range of typical materials found in PWR assemblies.
Footnotes
- Y. M. Chan and J. Dufek, “Representation of multi-group cross section libraries and flux spectra for PWR materials with deep neural networks for lattice calculations,” Annals of Nuclear Energy, vol. 208, 2024 ↩︎