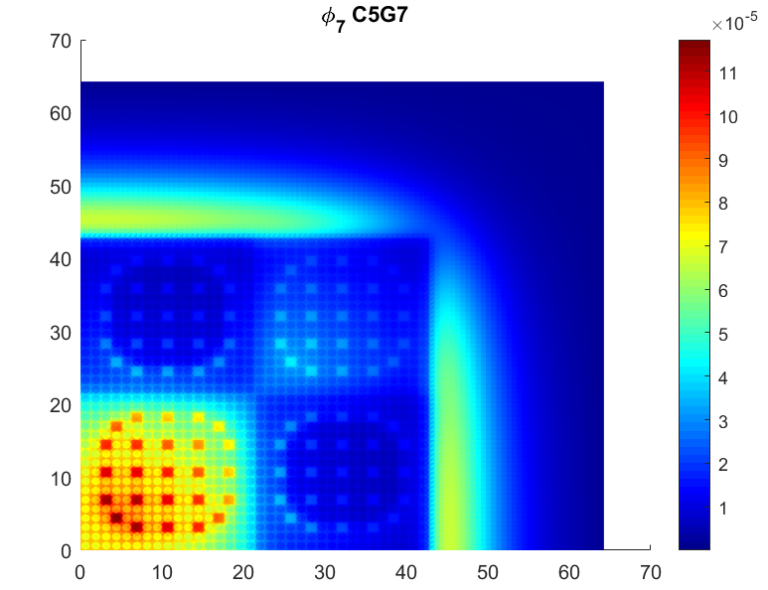
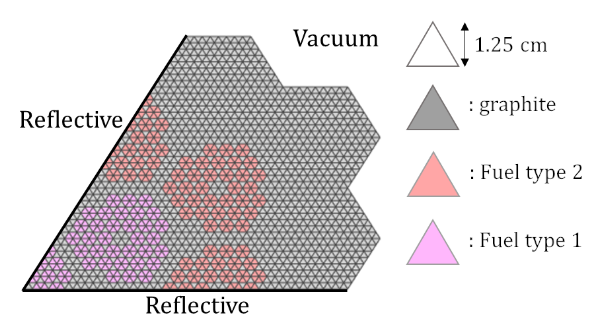
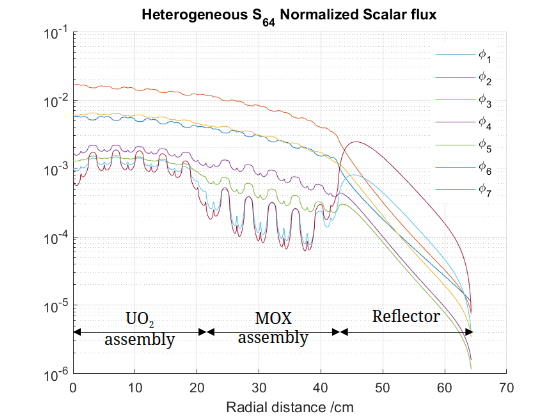
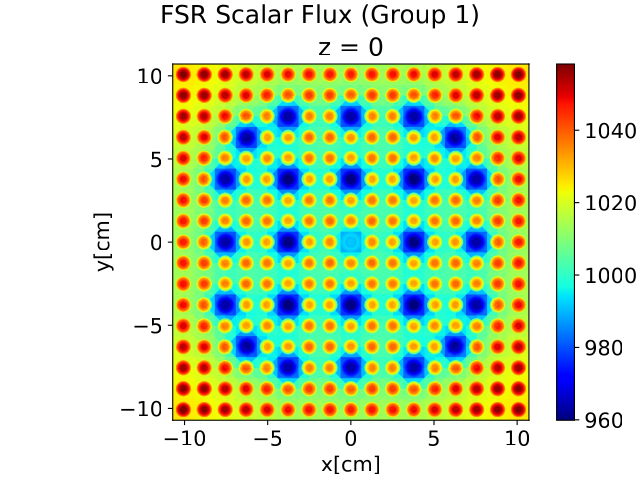
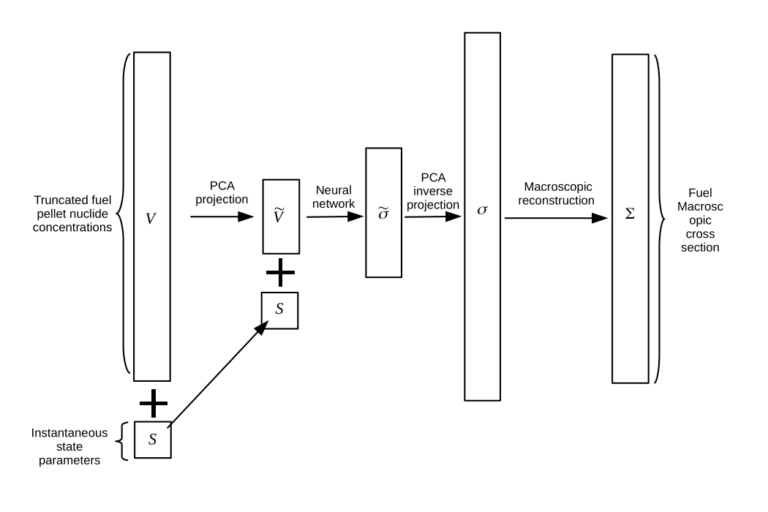
Paper summary: Machine learning approach for predicting nuclide composition in nuclear fuel: bypassing traditional depletion and transport calculations
Paper summary: Machine learning approach for predicting nuclide composition in nuclear fuel: bypassing traditional depletion and transport calculations Introduction This post is an informal summary of the paper “Machine learning approach for predicting nuclide composition in nuclear fuel: bypassing traditional depletion and transport calculations” published in Annals of Nuclear Energy in December 2024. In this […]